|
|
|||||||||||||||||||||||||||||||||||||||||||
RESOLUCIÓN DE
|
| (1) |
Se establece en matemáticas que en su solución general deben aparecer n constantes arbitrarias. Entonces, puede aceptarse que la solución general de (1) es:
| G(X, Y, C1, C 2, ... , C n) = 0 | (2) |
Gráficamente esta ecuación representa una familia de curvas planas, cada una de ellas obtenidas para valores particulares de las n constantes, C1, C2, ... , Cn, como se ve en la gráfica:
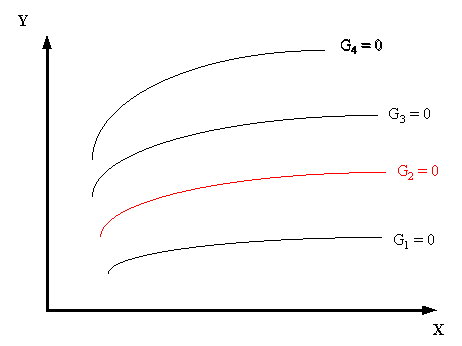
|
Fig. 1
Cada una de estas curvas corresponde a una solución particular de la ecuación diferencial (1) y analíticamente puede obtenerse sujetando la solución general (2) a n condiciones independientes que permiten valuar las constantes arbitrarias.
Dependiendo de como se establezcan estas condiciones, se distinguen dos tipos de problemas: los llamados de Valores Iniciales y los de Valores en la Frontera.
Un problema de valores iniciales está gobernado por una ecuación diferencial de orden n y un conjunto de n condiciones independientes todas ellas, válidas para el mismo punto inicial. Si la ecuación (1) es la ecuación diferencial que define el problema, y X = a es el punto inicial, puede aceptarse que las n condiciones independientes son:
|
|
(3) |
Se tratará de obtener una solución particular de (1) que verifique (3) como se presenta en la gráfica
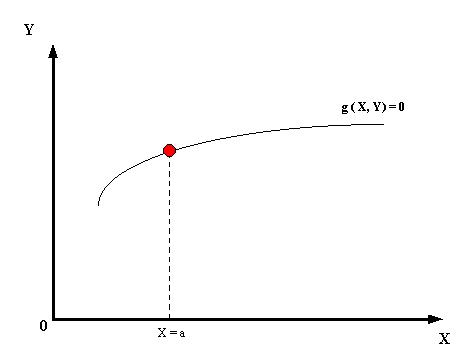
|
Fig. 2
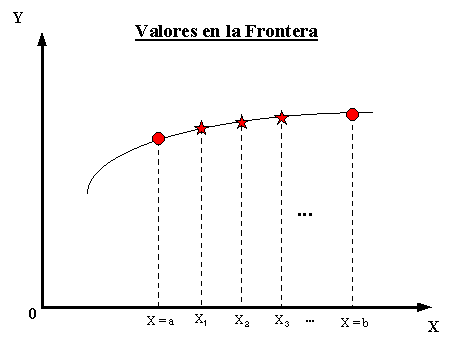
Por el contrario, en los problemas de valores en la
frontera deben establecerse condiciones de frontera en
todos y cada uno de los puntos que constituyen la
frontera del dominio de soluciones del problema.
En particular en el espacio de una dimensión, hay dos
puntos frontera, por ejemplo, X = a y X = b,
si el dominio de soluciones es el intervalo
cerrado ![]() ; por esto
mismo el orden mínimo de la ecuación diferencial de
un problema de valores en la frontera será dos y
como podemos observar en la siguiente gráfica:
; por esto
mismo el orden mínimo de la ecuación diferencial de
un problema de valores en la frontera será dos y
como podemos observar en la siguiente gráfica:
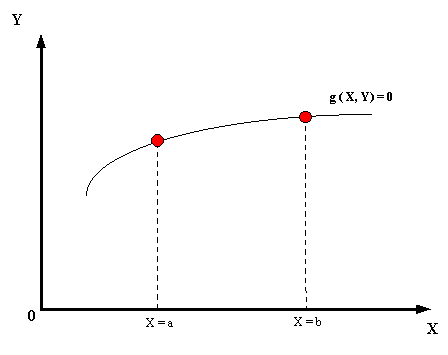
|
Fig. 3
Básicamente la solución numérica de ecuaciones diferenciales consiste en sustituir el dominio continuo de soluciones por uno discreto formado por puntos aislados igualmente espaciados entre sí.
Así, en un problema de valores iniciales, el dominio
de definición de soluciones
![]() se
sustituye por el conjunto infinito numerable de puntos,
se
sustituye por el conjunto infinito numerable de puntos,
X0 = a, X 1 = X 0 + h, X 2 = X 0 + 2h, X 3 = X 0 + 3h, ...
y en el caso de valores en la frontera se sustituye el
intervalo ![]() por el conjunto
finito de puntos
por el conjunto
finito de puntos
X0 = a, X 1 = X 0 + h, X 2 = X 0 + 2h, ... , X n = X 0 + nh = b
obtenidos, al dividir el intervalo en n partes iguales.
La presentación gráfica muestra estas dos cosas:
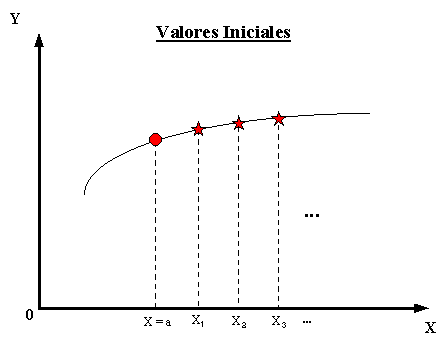
|
Fig. 4
|
Fig. 5
DISCRETIZACIÓN DEL DOMINIO DE DEFINICIÓN DE SOLUCIONES
Habiéndose discretizado el problema continuo, se tratará de obtener la solución para los puntos considerados, y esto se hará, en general, sustituyendo las derivadas que aparezcan en la ecuación diferencial con condiciones iniciales o en la frontera, por fórmulas numéricas de derivación que proporcionen aproximaciones a las derivadas o tratando de integrar la ecuación diferencial y reemplazando al proceso de integración por una fórmula numérica que se aproxime a la integral.
Una vez hecho esto, la ecuación obtenida expresada en diferencias finitas (ya que se han sustituido diferenciales por incrementos finitos) se aplica repetidamente en todos los puntos pivotes donde se desconoce la solución para llegar a una solución aproximada del problema.
SOLUCIÓN NUMÉRICA DE PROBLEMAS DE VALORES INICIALES
Un problema ordinario de valores iniciales está gobernado por una ecuación diferencial ordinaria y un conjunto de condiciones, todas ellas válidas para el mismo punto inicial, X=X0.
La solución numérica de este problema consiste en evaluar la integral de Y(X) en todos los puntos pivotes de su intervalo de definición, los que estarán igualmente espaciados en h unidades. Estos valores se obtienen paso a paso, a partir del punto inicial, lo que da el nombre de métodos de integración paso a paso.
La evaluación de Y en los puntos pivote
Xi = X0 + ih, para i = 1, 2, 3, ...
se lleva a cabo usando fórmulas de recurrencia, que usan los valores conocidos de Y en las estaciones anteriores.
Xi-1, Xi-2, Xi-3, ...
Así, para aplicar estas ecuaciones, es necesario entonces evaluar muy aproximadamente a Y(X) en algunos de los primeros puntos pivotes (uno a cuatro); y esto se hace usualmente desarrollando f(X) en serie de potencias.
EJEMPLO
Encuentre la solución del siguiente problema de valores iniciales por medio de los primeros cuatro términos de la serie de Taylor para X = 0.1, 0.2, 0.3, 0.4 y 0.5.
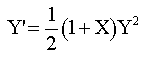
Y(0) = 1
SOLUCIÓN
Se obtienen las derivadas sucesivas :
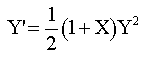
|
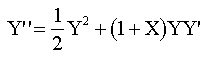
|
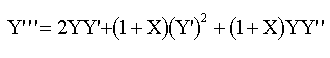
|
sustituyendo valores :

|
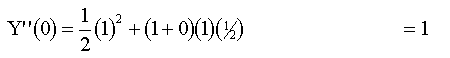
|
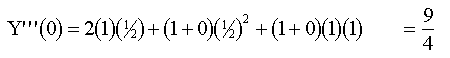
|
Por lo que:
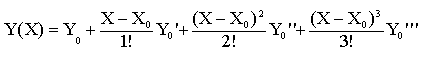
|
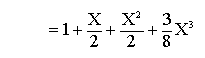
|
Evaluando para cada valor de X en esta última ecuación se tiene:
| X | Y | |
| 0 | 1 | |
| 0.1 | 1.055375 | |
| 0.2 | 1.123000 | |
| 0.3 | 1.205125 | |
| 0.4 | 1.304000 | |
| 0.5 | 1.421875 |