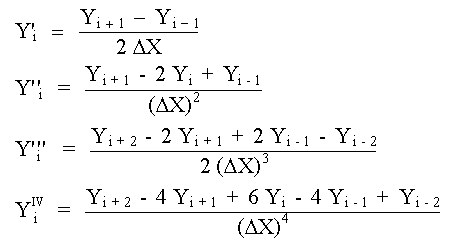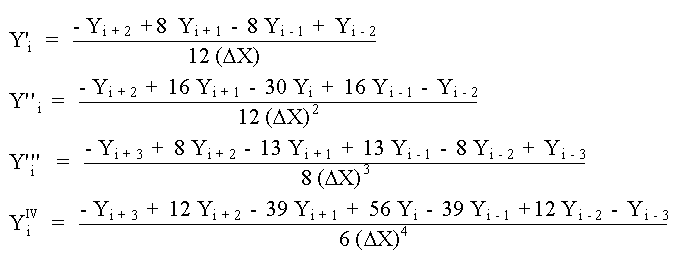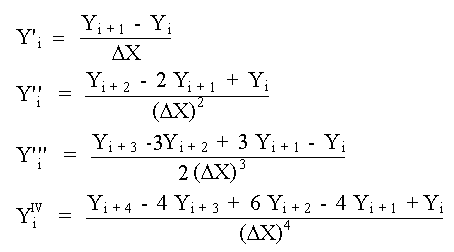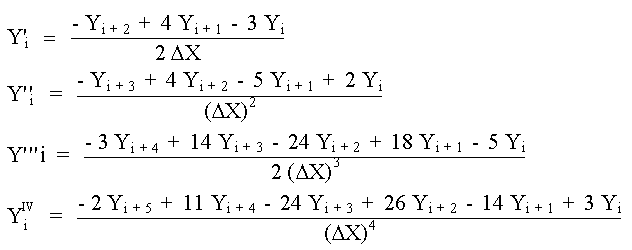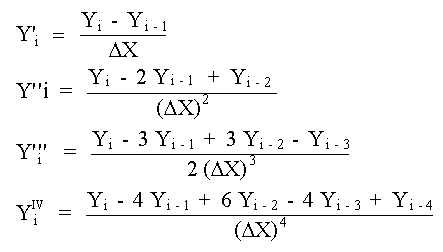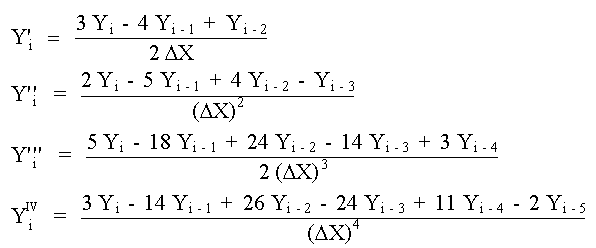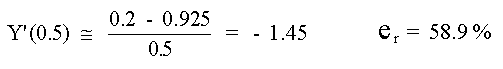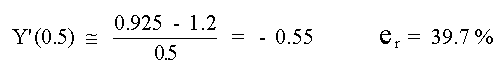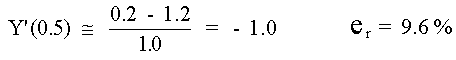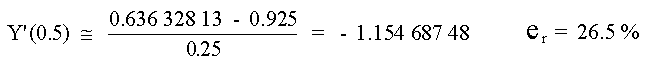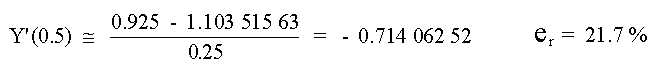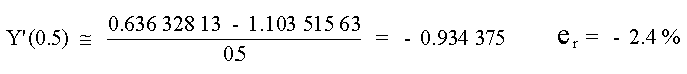DIFERENCIACIÓN NUMÉRICA

RESUMEN DE FÓRMULAS DE DIFERENCIACIÓN

Lo que sigue es un resumen de las fórmulas de diferenciación que se pueden obtener a base de desarrollos en serie de Taylor.

Expresiones de Primeras Diferencias Centrales

(12)

Expresiones de Segundas Diferencias Centrales

(13)

Expresiones de Primeras Diferencias Hacia Adelante

(14)

Expresiones de Segundas Diferencias Hacia Adelante

(15)

Expresiones de Primeras Diferencias Hacia Atrás

(16)

Expresiones de Segundas Diferencias Hacia Atrás

(17)

EJEMPLO

Úsense aproximaciones de Diferencias Finitas Hacia Adelante, Hacia Atrás y Centradas para estimar la primera derivada de:

utilizando un tamaño de paso de = 0.5.

Repetir los cálculos usando = 0.25.

Nótese que la derivada se puede calcular directamente como:

y evaluando tenemos:

f'(0.5) = -0.9125

SOLUCIÓN:

Para = 0.5 se puede usar la función para determinar:

Xi-1 = 0.0	Yi-1 = 1.200
Xi = 0.5	Yi = 0.925
Xi+1 = 1.0	Yi+1 = 0.200

Estos datos se pueden utilizar para calcular la Diferencia Hacia Adelante:

la Diferencia Dividida Hacia Atrás será:

y la Diferencia Dividida Central:

Para = 0.25, los datos son:

Xi-1 = 0.25	Yi-1 = 1.10351563
Xi = 0.50	Yi = 0.92500000
Xi+1 = 0.75	Yi+1 = 0.63632813

que se usarán para calcular la Diferencia Dividida Hacia Adelante:

la Diferencia Dividida Hacia Atrás:

y la Diferencia Dividida Central:

Para los dos tamaños de paso, las aproximaciones por Diferencias Centrales son más exactas que las Diferencias Divididas Hacia Adelante o las Diferencias Divididas Hacia Atrás. También, como lo predijo el análisis de la serie de Taylor, la división del intervalo en dos partes iguales, divide a la mitad el error de las Diferencias Hacia Atrás o Hacia Adelante y a la cuarta parte el error de las Diferencias Centrales.