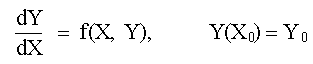|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
RESOLUCIÓN DE
|
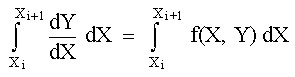 |
(4) |
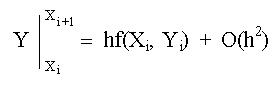
entonces
![]()
de donde se obtiene la siguiente expresión aproximada llamada fórmula de Euler
| Yi+1 = Yi + h f(Xi, Yi) | (5) |
EJEMPLO
Resolver el problema del ejemplo anterior aplicando el método de Euler.
Se tiene
Yi+1 = Yi + h f(Xi, Yi)
donde
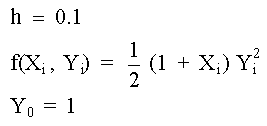
entonces
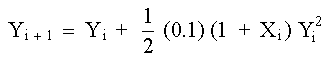
|
(6) |
En la tabla aparecen tabulados los valores de la solución aproximada obtenidos a partir de la condición inicial conocida Y0(0) = 1
| Xi | Yi | Yi solución exacta |
| 0.0 | 1.000 000 | 1.000 000 |
| 0.1 | 1.050 000 | 1.055 409 |
| 0.2 | 1.110 638 | 1.123 596 |
| 0.3 | 1.184 649 | 1.208 459 |
| 0.4 | 1.275 870 | 1.315 789 |
| 0.5 | 1.389 819 | 1.454 545 |
MÉTODO DE RUNGE - KUTTA
En la sección anterior se estableció que el método de Euler para resolver la ecuación diferencial de primer orden
| Y' = f(X, Y) | (7) |
con la condición inicial
| Y(X0) = Y0 | (8) |
consiste en aplicar repetidamente la fórmula de recurrencia
| Yn+1 = Yn + h f(Xn, Yn) donde n = 1, 2, 3, ... | (9) |
para determinar la solución de la ecuación diferencial en
X = X1, X2, X3, ...
Sustituyendo la función f(X,Y) dada en (7), en (9), se tiene que
| Yn+1 = Yn + h Y'n | (10) |
expresión que indica que el método de Euler consiste gráficamente, en ir de un valor Yn conocido de la solución de la ecuación diferencial (7) en un punto, al siguiente por medio de la tangente T1 a la curva integral Y = Y(X) en el mismo punto de la solución conocida, como se muestra en la siguiente figura.
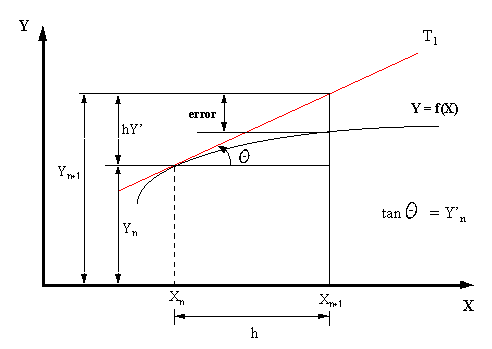
|
De este planteamiento gráfico puede verse que una mejor aproximación a la solución de la ecuación diferencial se obtendría si en vez de ir por la tangente T1 para determinar la solución en el siguiente Punto Pivote, se utiliza una secante con pendiente igual al promedio de pendientes de la curva integral en los puntos coordenados (Xn, Yn), (Xn+1, Yn+1) en donde Xn+1 y Yn+1 pueden estimarse con el procedimiento normal de Euler, como se muestra en la siguiente gráfica:
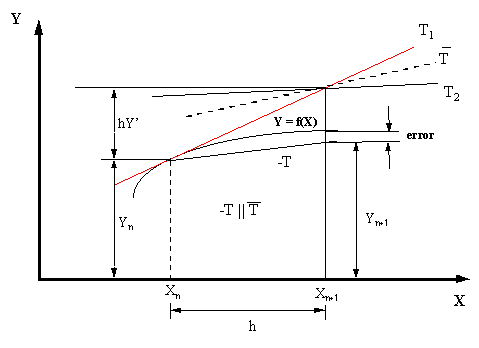
|
Con lo anterior se obtendría un método mejorado de
Euler con error del orden de
![]() definido
por la expresión
definido
por la expresión
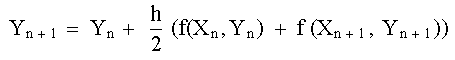
|
(11) |
en donde f(Xn+1, Yn+1) es el valor de la función f(X, Y) para:
X = Xn+1
Y = Yn + h f(Xn, Yn)
Observando las expresiones para resolver la ecuación diferencial, puede decirse que ambas consisten en aplicar la fórmula de recurrencia
|
|
(12) |
en donde
|
|
(13) |
en el método de Euler y
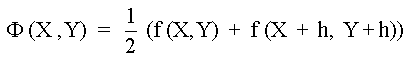
|
(14) |
en lo que
| Y' = f(X, Y) | (15) |
en el método de Euler Mejorado.
Como se ve, estos métodos tienen los siguientes puntos en común:
- Son métodos de un paso; para determinar Yn+1 se necesita conocer únicamente los valores de
Xn y Yn del punto anterior.
- No requieren evaluar ninguna derivada, sino únicamente valores de la función f(X, Y).
Estas características dan origen a una gran variedad
de métodos conocidos como de Runge-Kutta. La diferencia
entre ellos cosiste en la forma como se define
la función
![]() que aparece en la
expresión (12).
que aparece en la
expresión (12).
La ventaja de los métodos de Runge-Kutta con respecto al uso de la serie de Taylor, que es también un método de un paso, está expresado en el punto (2) anterior; es decir, los métodos de Runge-Kutta requieren sólo de la función f(X, Y) y de ninguna derivada, mientras que la serie de Taylor sí requiere de la evaluación de derivadas. Esto hace que, en la práctica, la aplicación de los métodos de Runge-Kutta sean más simples que el uso de la serie de Taylor.
Un método de Runge-Kutta para resolver ecuaciones diferenciales
ordinarias de primer orden con error del orden
de ![]() , de uso tan frecuente que en
la literatura sobre métodos numéricos se le llama simplemente
el Método de Runge-Kutta, se dará a conocer sin demostrar
y consiste en aplicar la ecuación de recurrencia (12) en donde
la función
, de uso tan frecuente que en
la literatura sobre métodos numéricos se le llama simplemente
el Método de Runge-Kutta, se dará a conocer sin demostrar
y consiste en aplicar la ecuación de recurrencia (12) en donde
la función
![]() está dada por
la expresión:
está dada por
la expresión:
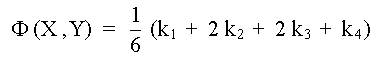
|
(16) |
en el cual
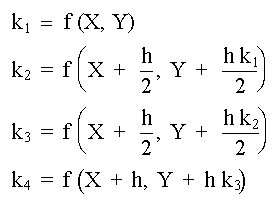
|
(17) |
La ecuación (16) se obtiene haciendo un promedio de las cuatro pendientes, k1, k2, k3 y k4 a la curva integral, en forma semejante a como se procedió con las pendientes de las tangentes T1 y T2 que dieron lugar a (11)
EJEMPLO
Resolver
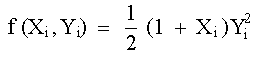
aplicando el método de Runge-Kutta.
SOLUCIÓN
De la condición inicial del problema se tiene que X = 0, y Y = 1; además, h = 0.1. Sustituyendo estos valores en (17) se obtiene:
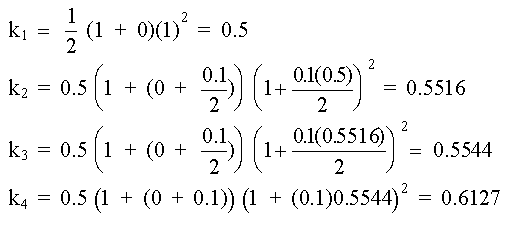
Llevando estos valores a (16) y el resultante a (12) se obtiene que para X = 0.1 la solución del problema es
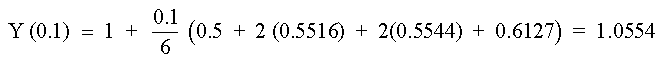
Los valores de las ki para este punto obtenido de la solución, son:
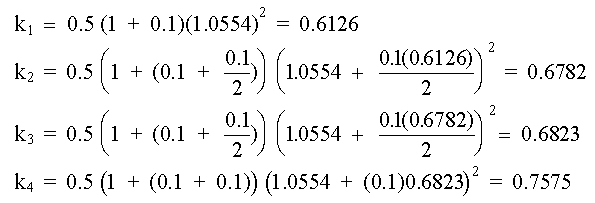
luego
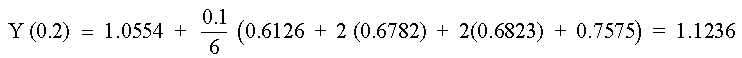
Continuando de la misma forma se obtiene la solución que se muestra en la siguiente tabla:
| X | Y | k1 | k2 | k3 | k4 |
| 0.0 | 1.0000 | 0.5000 | 0.5516 | 0.5544 | 0.6127 |
| 0.1 | 1.0554 | 0.6126 | 0.6782 | 0.6823 | 0.7575 |
| 0.2 | 1.1236 | 0.7575 | 0.8431 | 0.8494 | 0.9494 |
| 0.3 | 1.2085 | 0.9492 | 1.0647 | 1.0745 | 1.2121 |
| 0.4 | 1.3158 | 1.2119 | 1.3735 | 1.3896 | 1.5872 |
| 0.5 | 1.4545 | 1.5868 | 1.8234 | 1.8517 | 2.1509 |