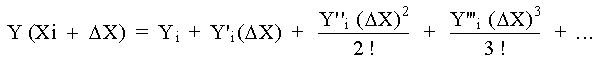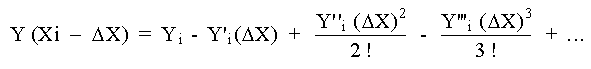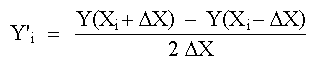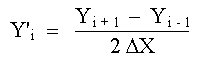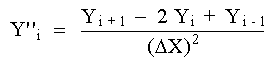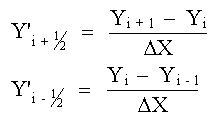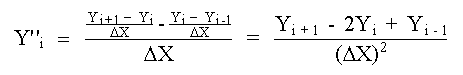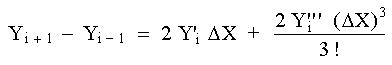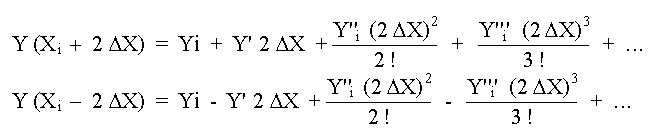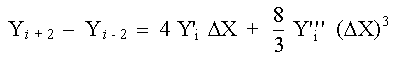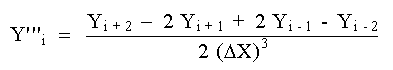DIFERENCIACIÓN NUMÉRICA

INTRODUCCIÓN

Concentremos ahora nuestra atención a procedimientos para diferenciar numéricamente funciones que están definidas mediante datos tabulados o mediante curvas determinadas en forma experimental.

Un método consiste en aproximar la función en la vecindad del punto en que se desea la derivada, mediante una parábola de segundo, tercer o mayor grado, y utilizar entonces la derivada de la parábola en ese punto como la derivada aproximada de la función.

Otro ejemplo, que comentaremos aquí, utiliza los desarrollos en serie de Taylor.

La serie de Taylor para una función Y = f(X) en , desarrollada con respecto al punto Xi es

(1)

en donde Yi es la ordenada que corresponde a Xi y se encuentra en la región de convergencia. La función para está dada en forma similar por:

(2)

Utilizando solamente los tres primeros términos de cada desarrollo, podremos obtener una expresión para Y'i restando la ec. (2) de la ec. (1),

(3)

DIFERENCIAS CENTRALES, HACIA ADELANTE Y HACIA ATRÁS

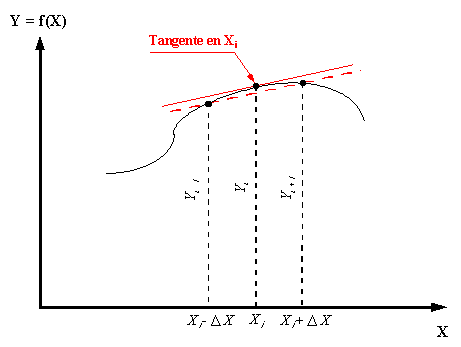
Observando la figura (1), vemos que si designamos los puntos uniformemente espaciados a la derecha de Xi como Xi+1 , Xi+2, etc. y los puntos a la izquierda de Xi como Xi-1, Xi-2 , etc. e identificamos las ordenadas correspondientes como Yi+1, Yi+2, Yi-1, Yi-2, respectivamente, la ec. (3) se puede escribir en la forma:

(4)

La ec. (4) se denomina la primera aproximación, por Diferencias Centrales de Y', para X. La aproximación representa gráficamente la pendiente de la recta discontinua mostrada en la figura 1. La derivada real se representa mediante la línea sólida dibujada como tangente a la curva en Xi.

Si sumamos las ecuaciones (1) y (2) y utilizamos la notación descrita previamente, podemos escribir la siguiente expresión para la segunda derivada:

(5)

La ec. (5) es la primera aproximación, por Diferencias Centrales, de la segunda derivada de la función en Xi. Esta expresión se puede interpretar gráficamente como la pendiente de la tangente a la curva en Xi+1/2 menos la pendiente de la tengente a la curva en Xi-1/2 dividida entre , cuando las pendientes de las tangentes están aproximadas mediante las expresiones:

(6)

es decir,

(7)

Para obtener una expresión correspondiente a la tercera derivada, utilizamos cuatro términos en el segundo miembro de cada una de las ecs. (1) y (2). Restando la ec. (2) de la ec. (1) se obtiene:

(8)

Si desarrollamos la serie de Taylor respecto a Xi para obtener expresiones correspondientes a Y = f(X) en y , respectivamente, obtenemos:

(9)

Restando la primera ec. (9) de la segunda, y utilizando solamente los cuatro términos mostrados para cada desarrollo, se obtiene:

(10)

La solución simultánea de las ecs. (8) y (10) produce la tercera derivada:

(11)

La ec. (11) es la primera expresión de Diferencias Centrales correspondiente a la tercera derivada de Y en Xi.

Por este método se pueden obtener derivadas sucesivas de mayor orden, pero como requieren la solución de un número cada vez mayor de ecuaciones simultáneas, el proceso se vuelve tedioso. La misma técnica se puede utilizar también para encontrar expresiones más precisas de las derivadas utilizando términos adicionales en el desarrollo en serie de Taylor. Sin embargo, la derivación de expresiones más precisas, especialmente para derivadas de orden superior al segundo, se vuelve muy laboriosa debido al número de ecuaciones simultáneas que se deben resolver.

No se presentan aquí esas derivaciones, pero dichas expresiones, para diferentes derivadas, se incluyen en el resumen que sigue a estos comentarios.

Las expresiones correspondientes a las derivadas de mayor orden se logran con mucho mayor facilidad y bastante menos trabajo, utilizando operadores de diferencias, de promedios y de derivación. Este método se encuentra fuera de los alcances fijados, pero se pueden encontrar en varios libros referentes al análisis numérico.

Se ha demostrado que las expresiones de Diferencias Centrales para las diversas derivadas encierran valores de la función en ambos lados del valor X en que se desea conocer la derivada en cuestión. Utilizando desarrollos convenientes en serie de Taylor, se pueden obtener fácilmente expresiones para las derivadas, completamente en términos de valores de la función en Xi y puntos a la derecha de Xi. Estas se conocen como expresiones de Diferencias Finitas Hacia Adelante.

En forma similar, se pueden obtener expresiones para las derivadas que estén totalmente en términos de valores de la función en Xi y puntos a la izquierda de Xi. Estas se conocen como expresiones de Diferencias Finitas Hacia Atrás.

En la diferenciación numérica, las expresiones de diferencias hacia adelante se utilizan cuando no se dispone de datos a la izquierda del punto en que se desea calcular la derivada, y las expresiones de diferencias hacia atrás, se utilizan cuando no se dispone de datos a la derecha del punto deseado. Sin embargo, las expresiones de diferencias centrales son más precisas que cualquiera de las otras dos.