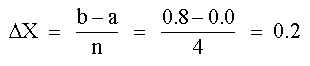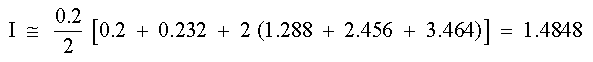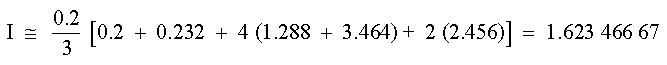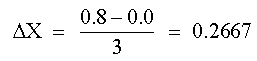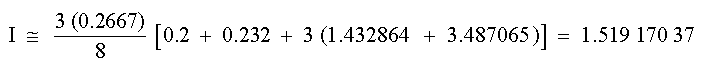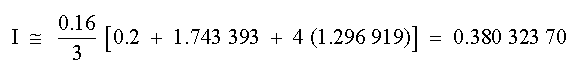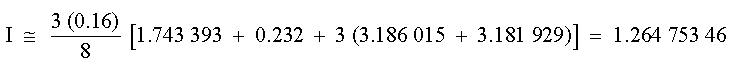INTEGRACIÓN NUMÉRICA

EJEMPLO 1

Utilícese la regla trapezoidal de cuatro segmentos o fajas para calcular la integral de

Fórmulas

desde a = 0 hasta b = 0.8 y calcular el error sabiendo que el valor correcto de la integral es 1.64053334.

 

SOLUCIÓN

n = 4

Fórmulas

X f(X)
0.0 0.200
0.2 1.288
0.4 2.456
0.6 3.464
0.8 0.232

usando la fórmula trapezoidal:

Fórmulas

ex = 1.64053334 - 1.4848 = 0.15573334

e% = 9.5 %

 

EJEMPLO 2

Utilícese la regla de Simpson de 1/3 con n = 4 para calcular la integral del inciso anterior

 

SOLUCIÓN

n = 4

Delta X = 0.2

X f(X)
0.0 0.200
0.2 1.288
0.4 2.456
0.6 3.464
0.8 0.232

usando la regla de Simpson de 1/3

Fórmulas

ex = 1.64053334 - 1.62346667 = 0.01706667

e% = 1.04 %

 

EJEMPLO 3

Utilícese la regla de Simpson de 3/8 para calcular la integral anterior:

SOLUCIÓN

Como se requieren cuatro puntos o tres fajas para la regla de Simpson de 3/8, entonces:

Fórmulas

X f(X)
0.0000 0.20000000
0.2667 1.43286366
0.5333 3.48706521
0.8000 0.23200000

usando la ecuación de Simpson de 3/8

Fórmulas

ex = 1.64053334 - 1.51917037 = 0.121164

e% = 7.4 %

 

EJEMPLO 4

Utilícese en conjunción las reglas de Simpson de 1/3 y 3/8 para integrar la misma función usando cinco segmentos.

SOLUCIÓN

Los datos necesarios para la aplicación de cinco segmentos (h = 0.16) son:

X f(X)
0.00 0.20000000
0.16 1.29691904
0.32 1.74339328
0.48 3.18601472
0.64 3.18192896
0.80 0.23200000

La integral de los primeros dos segmentos se obtiene usando la regla de Simpson de 1/3:

Fórmulas

Para los últimos tres segmentos, se usa la regla de Simpson de 3/8 para obtener:

Fórmulas

La integral total se calcula sumando los dos resultados:

I = 0.38032370 + 1.26475346 = 1.64507716

ex = 1.64053334 - 1.64507716 = -0.00454383

e% = -0.28 %