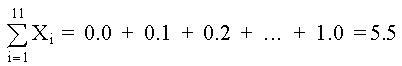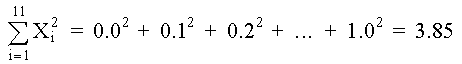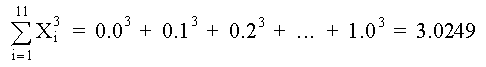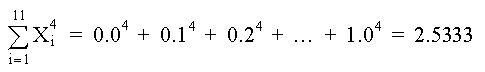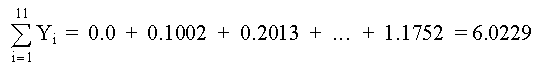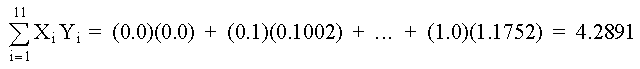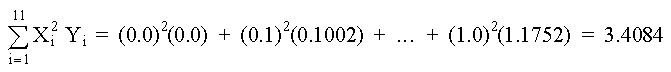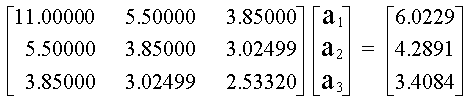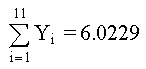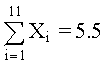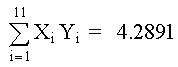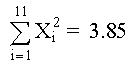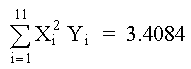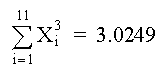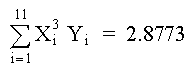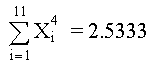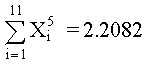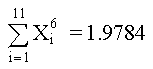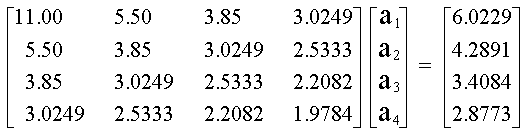AJUSTE DE CURVAS

De la tabla de datos, usando Mínimos Cuadrados, determine los polinomios de 2o, 3er y 4o grado; graficar para determinar la curva más aproximada.

SOLUCIÓN

POLINOMIO DE SEGUNDO GRADO

Primero determinamos los coeficientes de la matriz y los elementos constantes. Los elementos de la matriz son:

M =11

Los términos constantes son:

De acuerdo con esto, el sistema de ecuaciones a resolver es el siguiente:

Resolviendo por Gauss se obtienen los siguientes resultados.

y el polinomio de segundo grado es:

POLINOMIO DE TERCER GRADO

Para el caso del polinomio de 3er grado se requiere:

M =11

y el sistema de ecuaciones a resolver es:

cuya solución es:

y el polinomio queda:

POLINOMIO DE CUARTO GRADO

Repitiendo el procedimiento anterior, se obtienen los siguientes resultados

quedando el polinomio como se muestra: