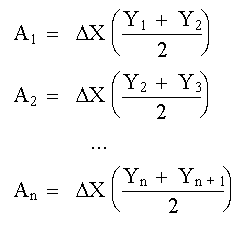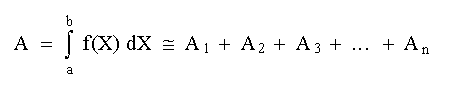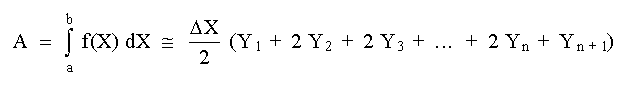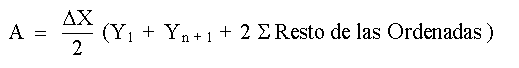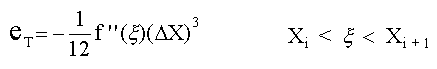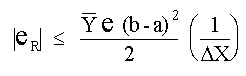|
|
|||||||||||||||||||
INTEGRACIÓN NUMÉRICAINTRODUCCIÓNEn ingeniería se presenta con frecuencia la necesidad de integrar una función que sería, en general, de una de las tres formas siguientes:
En el primer caso, la integral simplemente es una función que se puede evaluar fácilmente usando métodos analíticos aprendidos en el cálculo. En los dos últimos casos, sin embargo, se deben emplear métodos aproximados. Las fórmulas de integración de Newton-Cotes son los esquemas más comunes dentro de la integración numérica. Se basan en la estrategia de reemplazar una función complicada o un conjunto de datos tabulares con alguna función aproximada que sea más fácil de integrar. La integral se puede aproximar usando una serie de polinomios aplicados por partes a la función o a los datos sobre intervalos de longitud constante. Se dispone de las formas abierta y cerrada de las fórmulas de Newton-Cotes. Las formas cerradas son aquellas en donde los puntos al principio y al final de los límites de integración se conocen. Las fórmulas abiertas tienen los límites de integración extendidos más allá del rango de los datos. Las fórmulas abiertas de Newton-Cotes, en general, no se usan en la integración definida. Sin embargo, se usan extensamente en la solución de ecuaciones diferenciales ordinarias. REGLA DEL TRAPECIOLa regla del trapecio o regla trapezoidal es una de las fórmulas cerradas de Newton-Cotes.
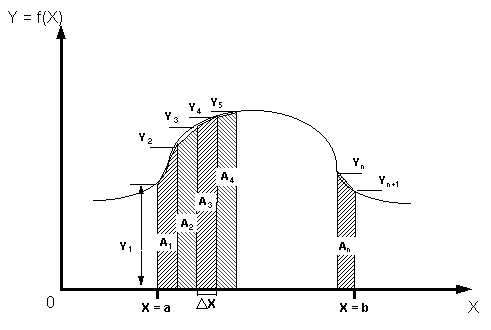
Considérese la función f(X),
cuya gráfica entre los extremos X = a y
X = b se muestra en la fig. 1.
Una aproximación suficiente al área bajo la curva
se obtiene dividiéndola en n fajas de ancho
Fig. 1 Llamando a las ordenadas Y i (i = 1, 2, 3, ...., n+1), las áreas de los trapecios son:
El área total comprendida entre X = a y X = b está dada por:
Sustituyendo las ecs. (1) en esta expresión se obtiene:
La cual recibe el nombre de Fórmula Trapezoidal, y se puede expresar como:
En esencia, la técnica consiste en dividir el intervalo total en intervalos pequeños y aproximar la curva Y = f(X) en los diversos intervalos pequeños mediante alguna curva más simple cuya integral puede calcularse utilizando solamente las ordenadas de los puntos extremos de los intervalos. Si la función f(X) se puede expresar como una función matemática continua que tiene derivadas continuas f'(X) y f''(X), el error que resulta de aproximar el área verdadera en una faja bajo la curva f(X) comprendida entre Xi y Xi+1 mediante el área de un trapecio, se demuestra que es igual a:
Este error es la cantidad que se debe agregar al área del
trapecio para obtener el área real. Se llama Error por
Truncamiento, ya que es el error que resulta de utilizar una
serie de Taylor truncada, en vez de una serie de Taylor completa,
para representar en forma de serie el área de una faja.
Generalmente no se puede valuar directamente el término mostrado
como error por truncamiento. Sin embargo, se puede obtener una
buena aproximación de su valor para cada faja suponiendo
que f '' es suficientemente constante en el intervalo de
la faja (se supone que las derivadas de orden superior son despreciables)
y evaluando f '' para
Otro error que se introduce al obtener el área aproximada de cada faja es el Error por Redondeo. Este se produce cuando las operaciones aritméticas requeridas se efectúan con valores numéricos que tienen un número limitado de dígitos significativos. Se puede demostrar que una aproximación a el límite del error por redondeo es:
Tenemos entonces que el límite en el error por redondeo
aumenta proporcionalmente a
El error por redondeo se puede minimizar utilizando aritmética de doble precisión o mediante compiladores que pueden manejar un gran número de dígitos significativos. De la información anterior se puede ver que el error total en el intervalo de integración deseado, es la suma de los errores de truncamiento y redondeo. Si el error total se debiera únicamente al error por truncamiento, se podría hacer tan pequeño como se deseara reduciendo suficientemente el ancho de la faja. Por ejemplo, bisectando el ancho de la faja se duplicaría el número de errores por truncamiento que hay que sumar, pero la expresión para el error en cada faja indica que cada uno sería aproximadamente un octavo de su valor previo. Sin embargo, disminuyendo el ancho de la faja se afectaría también el error total al aumentar el error por redondeo, debido al mayor número de operaciones que hay que efectuar al valuar la ec. (3). Entonces, cuando se disminuye el ancho de la faja para disminuir el error total, existe un punto óptimo en el cual disminuciones adicionales del ancho de la faja harían que el error aumentara en lugar de disminuir, porque el error por redondeo se volvería dominante. El ancho óptimo de la faja para una función especial se puede determinar fácilmente en forma experimental en la computadora (suponiendo que el área real bajo la gráfica de la función se puede valuar) pero es difícil definirlo analíticamente.
| |||||||||||||||||||