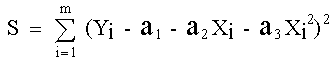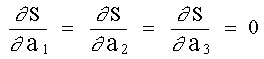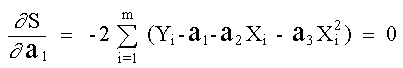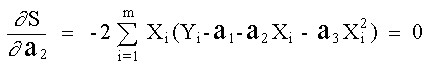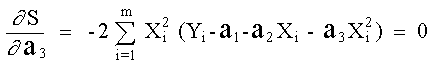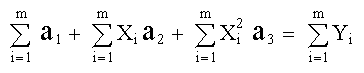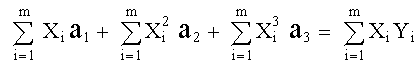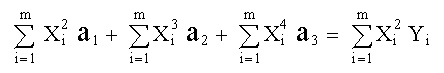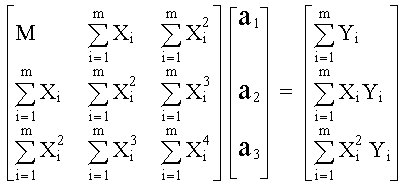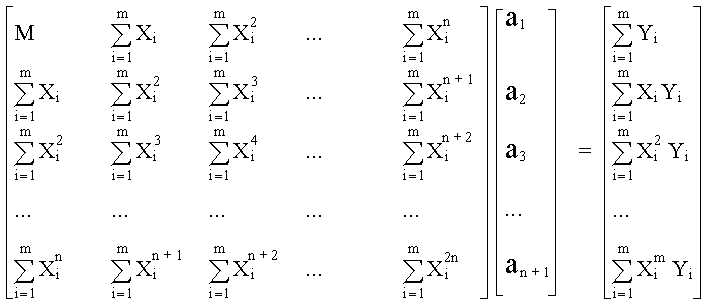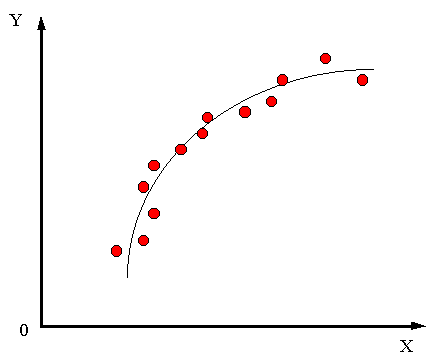
AJUSTE DE CURVAS

INTRODUCCIÓN

Supongamos que tenemos un conjunto de puntos que mostramos en la siguiente gráfica

De los puntos mostrados nos podemos dar cuenta que parece tener la forma de un polinomio de segundo grado de la forma:

(1)

Esta ecuación (1) puede usarse para representar el conjunto de valores obtenidos experimentalmente para la cual debemos determinar los valores de a 1, a 2, a 3, etc.

Para determinar estos valores utilizamos el siguiente procedimiento:

1. Establecer el criterio para determinar la ecuación que represente a los valores (obtenidos experimentalmente).

2. Escribir la ecuación que expresa el error o desviación entre el valor observado y los valores dados por la ecuación.

3. Habiendo obtenido la ecuación del error, minimizar dicho error.

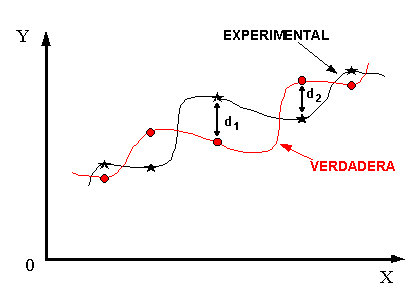
EVALUACIÓN DEL ERROR

Si consideramos las parejas de datos, como se muestra en la gráfica

donde:

d = distancia = Yobservada - Y obtenida por la ecuación

Yobservada = Valor obtenido experimentalmente.

Y obtenida por la ecuación = valor de la función evaluada en cualquier valor X

Observando la gráfica, parece que esta distancia se puede usar para representar el error, pero habrá distancias positivas y negativas, (como se puede observar la distancia d1 es positiva y la distancia d2 es negativa) de modo que el error promedio para los puntos como los mostrados será pequeño aunque los errores individuales sean grandes.

Esta dificultad podría ser resuelta usando el valor absoluto de las distancias, sin embargo al derivar la función del valor absoluto se generan ciertos problemas.

La solución podría ser definir el error como el cuadrado de la distancia, esto elimina la dificultad del signo. Por esta razón el método se llama: Método de Mínimos Cuadrados.

(2)

en donde S es la suma de los cuadrados de las diferencias entre el valor calculado y el valor observado y por lo tanto es el valor que se debe minimizar

(3)

Siendo el caso de que la curva supuesta es una ecuación de segundo grado, se tiene la ecuación:

(4)

Para minimizar la función anterior, derivando parcialmente con respecto a a 1, a 2 y a 3 e igualando a cero:

(5)

(Obsérvese que las variables son a 1, a 2 y a 3, mientras que Yi, X i son constantes)

Las ecuaciones se pueden expresar de acuerdo como sigue:

(6)

Lo anterior lo podemos expresar en forma matricial:

(7)

La fórmula general para un polinomio de grado n en donde hay m parejas de datos es:

(8)

Como se puede observar el problema consiste en lo siguiente:

1. Obtener la matriz de coeficientes.

2. Resolver el sistema de ecuaciones resultantes.

Recordando que:

1. Si n es el grado del polinomio, hay n+1 valores de la matriz de coeficientes y n+1 ecuaciones.

2. El máximo exponenete de X en los términos de la sumatoria de 2n puede ser que los datos no representen un polinomio de 2o grado sino que representen uno de 3o y 4o grados.

El ajuste de curvas es un procedimiento de tanteo y error, si una curva no representa los datos, entonces se intenta con un polinomio de grado superior.