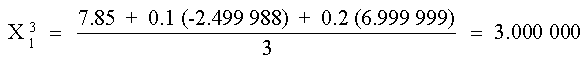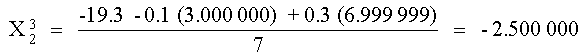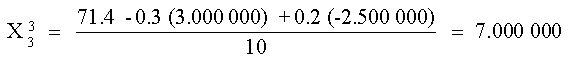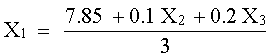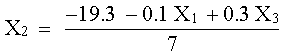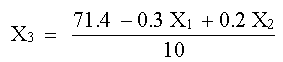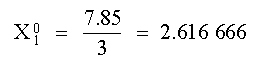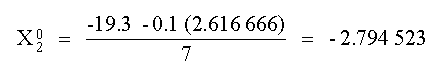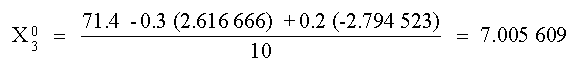RESOLUCIÓN DE SISTEMAS
DE ECUACIONES LINEALES
MÉTODO DE GAUSS-SEIDEL
El método de eliminación para resolver
ecuaciones simultáneas suministra soluciones suficientemente
precisas hasta para 15 o 20 ecuaciones. El número exacto
depende de las ecuaciones de que se trate,
del número de dígitos que se conservan en el
resultado de las operaciones aritméticas, y del
procedimiento de redondeo. Utilizando ecuaciones de error,
el número de ecuaciones que se pueden manejar se puede
incrementar considerablemente a más de 15 o 20, pero
este método también es impráctico cuando
se presentan, por ejemplo, cientos de ecuaciones que se deben
resolver simultáneamente. El método de inversión de
matrices tiene limitaciones similares cuando se trabaja
con números muy grandes de ecuaciones simultáneas.
Sin embargo, existen varias técnicas que se pueden
utilizar, para resolver grandes números de
ecuaciones simultáneas. Una de
las técnicas más útiles es
el método de Gauss-Seidel. Ninguno de los procedimientos
alternos es totalmente satisfactorio, y el método de
Gauss-Seidel tiene la desventaja de que no siempre converge a
una solución o de que a veces converge muy lentamente.
Sin embargo, este método convergirá siempre a
una solución cuando la magnitud del coeficiente de
una incógnita diferente en cada ecuación del
conjunto, sea suficientemente dominante con respecto a las
magnitudes de los otros coeficientes de esa ecuación.
Es difícil definir el margen mínimo por el que
ese coeficiente debe dominar a los otros para asegurar la
convergencia y es aún más difícil predecir
la velocidad de la convergencia para alguna combinación de valores
de los coeficientes cuando esa convergencia existe. No obstante, cuando
el valor absoluto del coeficiente dominante para
una incógnita diferente para cada ecuación es mayor
que la suma de los valores absolutos de los otros coeficientes de
esa ecuación, la convergencia está asegurada. Ese
conjunto de ecuaciones simultáneas lineales se conoce
como sistema diagonal.
Un sistema diagonal es condición suficiente para
asegurar la convergencia pero no es condición necesaria.
Afortunadamente, las ecuaciones simultáneas lineales que se
derivan de muchos problemas de ingeniería, son del tipo
en el cual existen siempre coeficientes dominantes.
La secuencia de pasos que constituyen
el método de Gauss-Seidel es la siguiente:
- 1. Asignar un valor inicial a cada incógnita que aparezca
en el conjunto. Si es posible hacer una hipótesis razonable
de éstos valores, hacerla. Si no, se pueden asignar
valores seleccionados arbitrariamente. Los
valores iniciales utilizados no afectarán la convergencia
como tal, pero afectarán el número de iteraciones
requeridas para dicha convergencia.
- 2. Partiendo de la primera ecuación, determinar un nuevo
valor para la incógnita que tiene el
coeficiente más grande en esa ecuación, utilizando
para las otras incógnitas los valores supuestos.
- 3. Pasar a la segunda ecuación y determinar en ella
el valor de la incógnita que tiene el
coeficiente más grande en esa ecuación, utilizando
el valor calculado para la incógnita del paso 2 y los
valores supuestos para las incógnitas restantes.
- 4. Continuar con las ecuaciones restantes, determinando siempre
el valor calculado de la incógnita que tiene el
coeficniente más grande en cada ecuación particular, y
utilizando siempre los últimos valores calculados para las
otras incógnitas de la ecuación. (Durante la
primera iteración, se deben utilizar los valores supuestos
para las incógnitas hasta que se obtenga un valor calculado).
Cuando la ecuación final ha sido resuelta, proporcionando
un valor para la única incógnita, se dice que se
ha completado una iteración.
- 5. Continuar iterando hasta que el valor de
cada incógnita, determinado en una iteración particular,
difiera del valor obtenido en la iteración previa,
en una cantidad menor que cierto
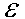 seleccionado
arbitrariamente. El procedimiento queda entonces completo. seleccionado
arbitrariamente. El procedimiento queda entonces completo.
Refiriéndonos al paso 5, mientras menor sea la
magnitud del
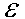 seleccionado,
mayor será la precisión de la solución. Sin
embargo, la magnitud del epsilon no especifica el error que
puede existir en los valores obtenidos para las incógnitas, ya
que ésta es una función de la velocidad de
convergencia. Mientras mayor sea la velocidad de convergencia,
mayor será la precisión obtenida en los valores de
las incógnitas para
un seleccionado,
mayor será la precisión de la solución. Sin
embargo, la magnitud del epsilon no especifica el error que
puede existir en los valores obtenidos para las incógnitas, ya
que ésta es una función de la velocidad de
convergencia. Mientras mayor sea la velocidad de convergencia,
mayor será la precisión obtenida en los valores de
las incógnitas para
un 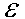 dado. dado.
EJEMPLO
Resolver el siguiente sistema de ecuación por el método Gauss-Seidel utilizando un
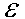 = 0.001. = 0.001.
0.1 X1 + 7.0 X2 - 0.3 X3 = -19.30
3.0 X1 - 0.1 X2 - 0.2 X3 = 7.85
0.3 X1 - 0.2 X2 - 10.0 X3 = 71.40
SOLUCIÓN:
Primero ordenamos las ecuaciones, de modo que en la diagonal
principal esten los coeficientes mayores para asegurar la convergencia.
3.0 X1 - 0.1 X2 - 0.2 X3 = 7.85
0.1 X1 + 7.0 X2 - 0.3 X3 = -19.30
0.3 X1 - 0.2 X2 - 10.0 X3 = 71.40
Despejamos cada una de las variables sobre la diagonal:
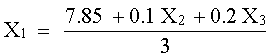
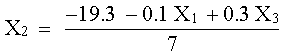
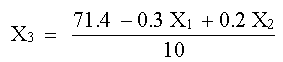
Suponemos los valores iniciales
X2 = 0 y
X3 = 0 y calculamos
X1
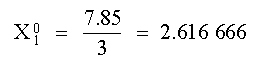
Este valor junto con el de X3 se puede utilizar
para obtener X2
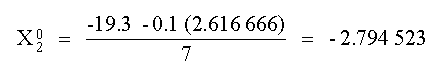
La primera iteración se completa sustituyendo los valores
de X1 y X2 calculados obteniendo:
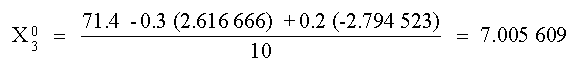
En la segunda iteración, se repite el mismo procedimiento:
Comparando los valores calculados entre la primera y la segunda
iteración
Como podemos observar, no se cumple la condición
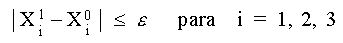
Entonces tomamos los valores calculados en
la última iteración y se toman como supuestos para
la siguiente iteración. Se repite entonces el proceso:
Comparando de nuevo los valores obtenidos
Como se observa todavía no se cumple la condición
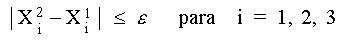
Así que hacemos otra iteración
Comparando los valores obtenidos
Dado que se cumple la condición, el resultado es:
| X1 = 3.0 |
| X2 = -2.5 |
| X3 = 7.0 |
Como se puede comprobar no se tiene un número exacto de
iteraciones para encontrar una solución. En este ejemplo, se
hicieron 3 iteraciones, pero a menudo se necesitan más iteraciones.
Se deja de investigación al alumno alguna forma que haga
que este método converga más rápidamente.
| 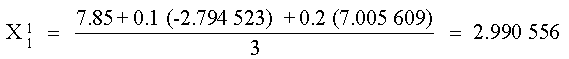
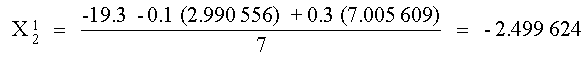
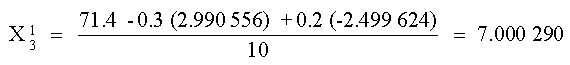
![]()
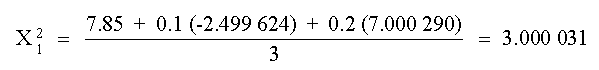
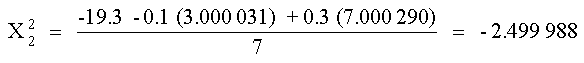
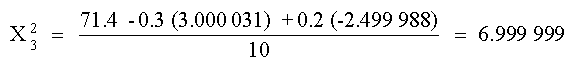
![]()