RESOLUCIÓN DE SISTEMAS
DE ECUACIONES LINEALES

MÉTODO DE ELIMINACIÓN DE GAUSS

El primer método que se presenta usualmente en álgebra, para la solución de ecuaciones algebricas lineales simultáneas, es aquel en el que se eliminan las incógnitas mediante la combinación de las ecuaciones. Este método se conoce como Método de Eliminación. Se denomina eliminación Gaussiana si en el proceso de eliminación se utiliza el esquema particular atribuido a Gauss.

Utilizando el método de Gauss, un conjunto de n ecuaciones con n incógnitas se reduce a un sistema triangular equivalente (un sistema equivalente es un sistema que tiene iguales valores de la solución), que a su vez se resuelve fácilmente por "sustitución inversa"; un procedimiento simple que se ilustrará con la presentación siguiente.

El esquema de Gauss empieza reduciendo un conjunto de ecuaciones simultáneas, tal como se muestra en (2), a un sistema triangular equivalente como:

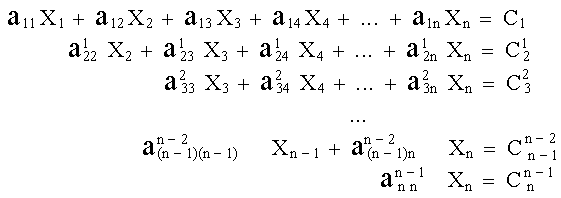
(6)

en el cual los superíndices indican los nuevos coeficientes que se forman en el proceso de reducción. La reducción real se logra de la siguiente manera:

1. La primera ecuación (2) se divide entre el coeficiente de X1 en esa ecuación para obtener:

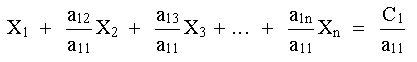
(7)

La ec. (7) se multiplica entonces por el coeficiente de X1 de la segunda ecuación (2) y la ecuación que resulta se resta de la misma, eliminando así X1. La ec. (7) se multiplica entonces por el coeficiente de X1 de la tercera ecuación (2), y la ecuación resultante se resta de la misma para eliminar X1 de esa ecuación. En forma similar, X1 se elimina de todas las ecuaciones del conjunto excepto la primera, de manera que el conjunto adopta la forma:

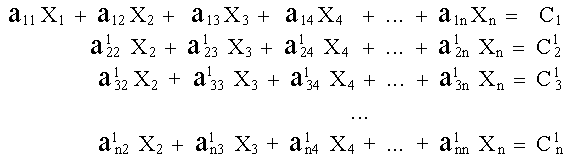(8)

La ecuación utilizada para eliminar las incógnitas en las ecuaciones que la siguen se denomina Ecuación Pivote. En la ecuación pivote, el coeficiente de la incógnita que se va a eliminar de las ecuaciones que la siguen se denomina el Coeficiente Pivote (a11 en los pasos previos).

2. Siguiendo los pasos anteriores, la segunda ecuación (8) se convierte en la ecuación pivote, y los pasos de la parte 1 se repiten para eliminar X2 de todas las ecuaciones que siguen a esta ecuación pivote.

Esta reducción nos conduce a:

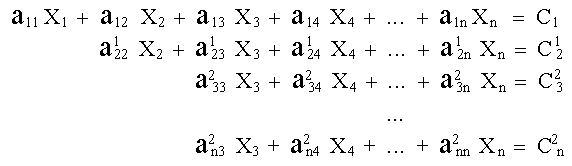
(9)

3. A continuación se utiliza la tercer ecuación (9) como ecuación pivote, y se usa el procedimiento descrito para eliminar X3 de todas las ecuaciones que siguen a la tercer ecuación (9). Este procedimiento, utilizando diferentes ecuaciones pivote, se continúa hasta que el conjunto original de ecuaciones ha sido reducido a un conjunto triangular tal como se muestra en la ec. (6).

4. Una vez obtenido el conjunto triangular de ecuaciones, la última ecuación de este conjunto equivalente suministra directamente el valor de Xn (ver ec. 6). Este valor se sustituye entonces en la antepenúltima ecuación del conjunto triangular para obtener un valor de Xn-1, que a su vez se utiliza junto con el valor de Xn en la penúltima ecuación del conjunto triangular para obtener un valor Xn-2 y asi sucesivamente. Este es el procedimiento de sustitución inversa al que nos referimos previamente.

Para ilustrar el método con un conjunto numérico, apliquemos estos procedimientos a la solución del siguiente sistema de ecuaciones:

Utilizando como ecuación pivote la primera ecuación (el coeficiente pivote es unitario), obtenemos:

A continuación, utilizando la segunda ecuación del sistema (11) como ecuación pivote y repitiendo el procedimiento, se obtiene el siguiente sistema triangular de ecuaciones:

Finalmente mediante sustitución inversa, comenzando con la última de las ecs. (12) se obtienen los siguientes valores:

DESVENTAJAS DEL MÉTODO DE ELIMINACIÓN

1. DIVISIÓN ENTRE CERO

Una de sus desventajas es que durante el proceso en las fases de eliminación y sustitución es posible que ocurra una división entre cero. Se ha desarrollado una estrategia del pivoteo para evitar parcialmente estos problemas. Ésta se deja como investigación al alumno.

2. ERRORES DE REDONDEO

La computadora maneja las fracciones en forma decimal con cierto número limitado de cifras decimales, y al manejar fracciones que se transforman a decimales que nunca terminan, se introduce un error en la solución de la computadora. Este se llama error por redondeo.

Cuando se va a resolver solamente un pequeño número de ecuaciones, el error por redondeo es pequeño y generalmente no se afecta sustancialmente la presición de los resultados, pero si se van a resolver simultáneamente muchas ecuaciones, el efecto acumulativo del error por redondeo puede introducir errores relativamente grandes en la solución. Por esta razón el número de ecuaciones simultáneas que se puede resolver satisfactoriamente con el método de eliminación de Gauss, utilizando de 8 a 10 dígitos significativos en las operaciones aritméticas, se limita generalmente a 15 o 20.

3. SISTEMAS MAL CONDICIONADOS

La obtención de la solución depende de la condición del sistema. En sentido matemático, los sistemas bien condicionados son aquellos en los que un cambio en uno o más coeficientes provoca un cambio similar en la solución. Los sistemas mal condicionados son aquellos en los que cambios pequeños en los coeficientes provocan cambios grandes en la solución.

Una interpretación diferente del mal condicionamiento es que un rango amplio de respuestas puede satisfacer aproximadamente al sistema. Ya que los errores de redondeo pueden inducir cambios pequeños en los coeficientes, estos cambios artificiales pueden generar errores grandes en la solución de sistemas mal condiconados.