|
|
||||||||||||||||||||||||||||||
RESOLUCIÓN DE SISTEMAS
|
| a 11 X1 + a 12 X2 + a 13 X3 + ... + a 1n Xn = C1 | (1) |
Es una ecuación algebraica lineal en las variables X1, X2, X3, ... , Xn. Se admite que los coeficientes a11, a12, a13, ... , a1n y el término independiente C1, son constantes reales.
SISTEMA DE ECUACIONES
Es un conjunto de ecuaciones que deben resolverse simultáneamente. En los sucesivo se considerarán únicamente sistemas de ecuaciones algebráicas lineales, o sea conjuntos de ecuaciones de la forma:
| a11 X 1 + a 12 X2 + a13 X 3 +... + a 1n X n = C 1 | (a) | |||
| a 21 X 1 + a 22 X 2 + a 23 X 3 +... + a 2n X n = C 2 | (b) | (2) | ||
| ... | ||||
| a n1 X 1 + a n2 X 2 + a n3 X 3 + ... + a nn X n = C n | (c) |
Aplicando la definición de producto entre matrices, este sistema de n ecuaciones algebraicas lineales con n incógnitas puede escribirse en forma matricial.
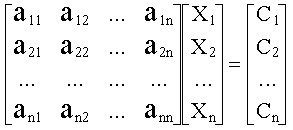 |
(3) |
Este sistema de ecuaciones puede escribirse simbólicamente como:
| A X = C | (4) |
en donde A se llama Matriz del Sistema. La matriz formada por A, a la que se le ha agregado el vector de términos independientes como última columna, se le llama la Matriz Ampliada del Sistema, que se representa con (A, C).
Entonces la matriz ampliada será:
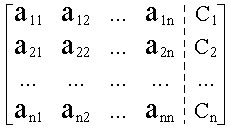 |
(5) |
SOLUCIÓN DE UN SISTEMA DE ECUACIONES
Es un conjunto de valores de las incógnitas que verifican simultáneamente a todas y cada una de las ecuaciones del sistema.
De acuerdo con su solución, un sistema puede ser: Consistente, si admite solución; o Inconsistente, si no admite solución.
Un sistema Consistente puede ser: Determinado, si la solución es única o Indeterminado, si la solución no es única. En este caso se demuestra que existe una infinidad de soluciones.
TEOREMAS SOBRE RANGOS
El rango de una matriz es el orden de determinante no nulo de mayor orden que puede obtenerse de esa matriz. El rango de la matriz A se representa con la notación r(A) y el de la matriz ampliada con r(A, C).
En álgebra se demuestra que:
- Para cualquier sistema,
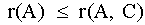
- Si r(A) < r(A, C) el sistema es inconsistente
- Si r(A) = r(A, C) el sistema de ecuaciones es consistente
En este caso, si además r(A) = n, el sistema es determinado e indeterminado si r(A) < n, siendo n el número de variables en el sistema.
En general, hay dos tipos de técnicas numéricas para resolver ecuaciones simultáneas: Directas, que son finitas; e Indirectas, que son infinitas.
Naturalmente, ninguna técnica práctica puede ser infinita. Lo que queremos decir es que en un principio los métodos directos (despreciando errores por redondeo) producirán una solución exacta, si la hay, en un número finito de operaciones aritméticas.
Por otra parte, un método indirecto requerirá en principio un número infinito de operaciones aritméticas para producir una solución exacta. Dicho de otra manera, un método indirecto tiene un error por truncamiento mientras que un método directo no lo tiene.
Sin embargo, la expresión "en principio" del párrafo anterior es crucial: en realidad se tienen errores por redondeo. Tendremos que considerar más cuidadosamente esta cuestión. En un sistema grande, mal comportado, los errores por redondeo de un método directo puede hacer que la "solución" carezca de sentido. A pesar de su error teórico por truncamiento, un método indirecto puede ser mucho más deseable porque en él los errores por redondeo no se acumulan.