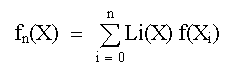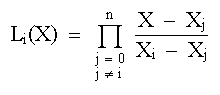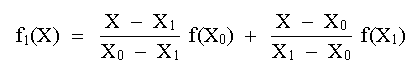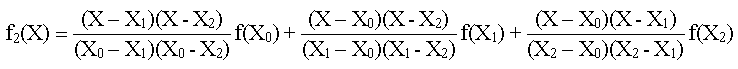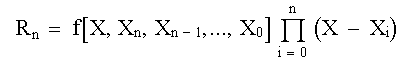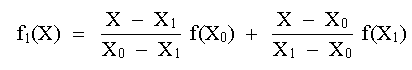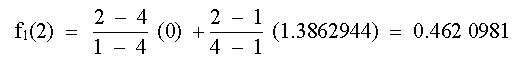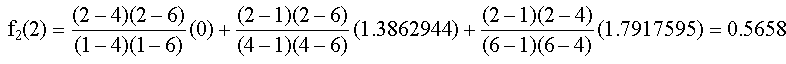INTERPOLACIÓN

POLINOMIOS DE INTERPOLACIÓN DE LAGRANGE

El polinomio de interpolación de Lagrange, simplemente es una reformulación del polinomio de Newton que evita los cálculos de las diferencias divididas. Este se puede representar concretamente como:

(21)

en donde:

(22)

En donde denota el "producto de".

Por ejemplo, la versión lineal (n = 1) es:

(23)

y la versión de segundo orden es:

(24)

al igual que en el método de Newton, la versión de Lagrange tiene un error aproximado dado por:

(25)

La ecuación (21) se deriva directemente del polinomio de Newton. Sin embargo, la razon fundamental de la formulación de Lagrange se puede comprender directamente notando que cada término Li(X) será 1 en X=Xi y 0 en todos los demas puntos.

Por lo tanto, cada producto Li(X) f(Xi) toma un valor de f(Xi) en el punto Xi. Por consiguiente la sumatoria de todos los productos, dada por la ecuación (21) es el único polinomio de n-ésimo orden que pasa exactamente por los n+1 puntos.

Ejemplo 3.4

Úsese un polinomio de interpolación de Lagrange de primer y segundo orden para evaluar ln 2 en base a los datos:

Solución:

El polinomio de primer orden es:

y, por lo tanto, la aproximación en X = 2 es

de manera similar, el polinomio de segundo orden se desarrolla como:

Como se expresaba, ambos resultados son similares a los que se obtuvieron previamente usando la interpolación polinomial de Newton.

En resumen, para los casos en donde el orden del polinomio se desconozca, el método de Newton tiene ventajas debido a que profundiza en el comportamiento de las diferentes fórmulas de orden superior. Ademas la aproximación del error dada por la ecuación (20), en general puede integrarse fácilmente en los cálculos de Newton ya que la aproximación usa una diferencia dividida. De esta forma, desde el punto de vista de cálculo, a menudo, se prefiere el método de Newton.

Cuando se va a llevar a cabo sólo una interpolación, ambos métodos, el de Newton y el de Lagrange requieren de un esfuerzo de calculo similar. Sin embargo, la versión de Lagrange es un poco más fácil de programar. T ambien existen casos en donde la forma de Newton es mas susceptible a los errores de redondeo. Debido a esto y a que no se requiere calcular y almacenar diferencias divididas, la forma de Lagrange se usa, a menudo, cuando el orden del polinomio se conoce a priori.