|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
INTERPOLACIÓNINTERPOLACIÓN POLINOMIAL DE LAS DIFERENCIAS FINITAS DE NEWTON
|
|
|
(11) |
Como se hizo anteriormente con las interpolaciones lineales y cuadráticas, se usan los puntos en la evaluación de los coeficientes b0, b1, ... , bn.
Se requieren n + 1 puntos para obtener un polinomio de n-ésimo orden: X0, X1, ... , Xn.
Usando estos datos, con las ecuaciones siguientes se evalúan los coeficientes:
| b0 = f (X0) | ||
| b1 = f [X1, X0] | ||
| b2 = f [X2, X1, X0] | (12) | |
| ... | ||
| bn = f [X n, Xn-1, ..., X1, X0] |
En donde las evaluaciones de la función entre corchetes son diferencias divididas finitas.
Por ejemplo, la primera diferencia dividida finita se representa generalmente como:
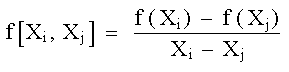
|
(13) |
La segunda diferencia dividida finita, que representa la diferencia de dos primeras diferencias divididas finitas, se expresa generalmente como:
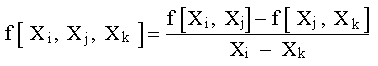
|
(14) |
De manera similar, la n-ésima diferencia dividida finita es:
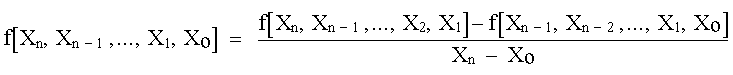
|
(15) |
Estas diferencias se usan para evaluar los coeficientes de la ecuación (12), los cuales se sustituyen en la ecuación (11), para obtener el polinomio de interpolación:
| f n (X) = f(X0) + (X-X0) f[X1, X0] + (X-X0)(X-X1) f[X2, X1, X0] + ...+ (X-X0)(X-X1)...(X-Xn-1) f[Xn, Xn-1,...,X1, X0] |
(16) |
Al cual se le llama Polinomio de Interpolación con Diferencias Divididas de Newton.
Se debe notar que no es necesario que los datos usados en la ecuación (16) estén igualmente espaciados o que los valores de la abscisa necesariamente se encuentren en orden ascendente, como se ilustra en el ejemplo 3.3
Todas las diferencias pueden arreglarse en una tabla de diferencias divididas, en donde cada diferencia se indica entre los elementos que la producen:
| i | Xi | f(Xi) | Primera | Segunda | Tercera |
| 0 | X0 | f(X0) | f(X1, X0) | f(X2, X1, X0) | f(X3, X2, X1, X0) |
| 1 | X1 | f(X1) | f(X2, X1) | f(X3, X2, X1) | |
| 2 | X2 | f(X2) | f(X3,X2) | ||
| 3 | X3 | f(X3) |
EJEMPLO 3.3
Usando la siguiente tabla de datos, calcúlese ln 2 con un polinomio de interpolación de Newton con diferencias divididas de tercer orden:
| X | f(X) |
| 1 | 0.000 0000 |
| 4 | 1.386 2944 |
| 6 | 1.791 7595 |
| 5 | 1.609 4379 |
SOLUCIÓN:
El polinomio de tercer orden con n = 3, es.
![]()
Las primeras diferencias divididas del problema son:
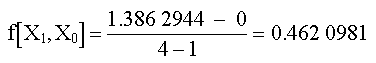
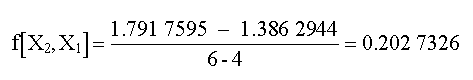
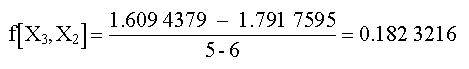
Las segundas diferencias divididas son:
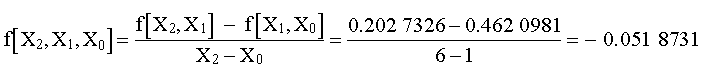
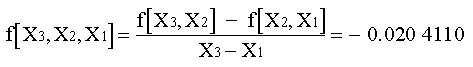
La tercera diferencia dividia es:
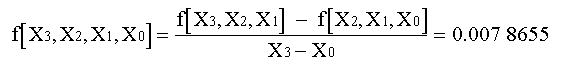
Los resultados para f(X1, X0), f(X2, X1, X0) y f(X3, X2, X1, X0) representan los coeficientes b1, b2 y b3 Junto con b0 = f (X0) = 0.0, la ecuación da:
f 3 (X) = 0 + 0.46209813 (X-1) - 0.0518731 (X-1)(X-4) + 0.0078655415 (X-1)(X-4)(X-6)
Arreglando la tabla de diferencias
| X | f [X] | f 1 [ ] | f 2 [ ] | f 3 [ ] |
| 1.0 | 0.00000000 | 0.46209813 | - 0.051873116 | 0.0078655415 |
| 4.0 | 1.3862944 | 0.20273255 | - 0.020410950 | |
| 6.0 | 1.7917595 | 0.18232160 | ||
| 5.0 | 1.6094379 |
Con la ecuación anterior se puede evaluar para X = 2
f 3 (2) = 0.62876869
lo que representa un error relativo porcentual del e% = 9.3%.
Nótese que la estructura de la ecuación (16) es similar a la expresión de la serie de Taylor en el sentido de que los términos agregados secuencialmente consideran el comportamiento de orden superior de la función representada. Estos términos son diferencias divididas finitas, y por lo tanto, representan aproximaciones a las derivadas de orden superior. En consecuencia, como sucede con la serie de Taylor, si la función representativa es un polinomio de n-ésimo orden, el polinomio interpolante de n-ésimo orden bajado en n + 1 llevará a resultados exactos.
El error por truncamiento de la serie de Taylor es:
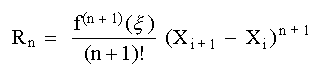
|
(17) |
en donde
![]() es un punto cualquiera dentro del intervalo (Xi, Xi+1). Una relación análoga del error en un polinomio interpolante de
n-ésimo orden está dado por:
es un punto cualquiera dentro del intervalo (Xi, Xi+1). Una relación análoga del error en un polinomio interpolante de
n-ésimo orden está dado por:
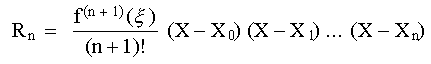
|
(18) |
En donde
![]() es un punto cualquiera dentro del intervalo que contiene las incógnitas y los datos. Para uso de esta fórmula la función en cuestión debe ser conocida
y diferenciable. Y usualmente, este no es el caso.
es un punto cualquiera dentro del intervalo que contiene las incógnitas y los datos. Para uso de esta fórmula la función en cuestión debe ser conocida
y diferenciable. Y usualmente, este no es el caso.
Afortunadamente existe una fórmula alternativa que no requiere conocimiento previo de la función. En vez de ello, se usa una diferencia dividida finita que aproxima la (n+1)-ésima derivada:
| Rn = f [X, Xn, Xn-1, ... , X1, X0](X-X0)(X-X1)..(X-Xn) | (19) |
en donde f(X, Xn, Xn-1, ... , X0) es la (n+1)-ésima diferencia dividida.
Ya que la ecuación (19) contiene la incógnita f(X), ésta no se puede resolver y obtener el error. Sin embargo, si se dispone de un dato adicional f(Xn+1), la ecuación (19) da una aproximación del error como:
|
|
(20) |