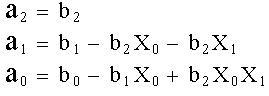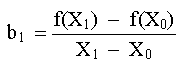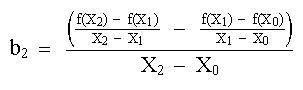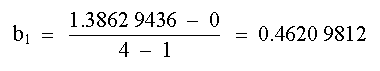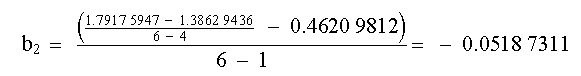INTERPOLACIÓN

INTERPOLACIÓN CUADRÁTICA

El error en el ejemplo 3.1 se debe a que se aproxima a una curva mediante una línea recta. Por consiguiente, una estrategia que mejora la aproximación es la de introducir cierta curvatura en a línea que conecta a los puntos. Si se dispone de tres puntos lo anterior se puede llevar a cabo con un polinomio de segundo orden (llamado también polinomio cuadrático o parábola). Una manera conveniente para este caso es:

(4)

Nótese que aunque la ecuación (4) parezca diferente de la ecuación general de un polinomio (1), las dos ecuaciones son equivalentes.

Esto se puede demostrar si se multiplican los términos de la ecuación (4) y obtener:

(5)

o, agrupar términos:

(6)

en donde:

(7)

De esta manera, las ecuaciones (1) y (4) son fórmulas alternativas equivalentes del único polinomio de segundo grado que une a los tres puntos.

Se puede usar un procedimiento simple para determinar los valores de los coeficientes. Para b0, se usa la ecuación (4) con X = X0, y se obtiene

b0 = f(X0)

(8)

sustituyendo la ecuación (8) en la ecuación (4) y evaluando en X = X1 se obtiene:

(9)

Y por último, las ecuaciones (8) y (9) se sustituyen en la ecuación (4), y se evalúa ésta en X = X2 y se obtiene:

(10)

Nótese que, al igual que en el caso de interpolación lineal, b1 aún representa la pendiente de la línea que une los puntos X0 y X1. Por lo tanto, los primeros dos términos de la ecuación (4) son equivalentes a la interpolación de X0 a X1, como se especificó anteriormente en la ecuación (3). El último término, b2(X-X0)(X-X1), introduce la curvatura de segundo orden en la fórmula.

Ejemplo 3.2

Ajústese el polinomio de segundo orden a los tres puntos usados en el ejemplo 3.1

X0 = 1		f (X0) = 0.0000 000
X1 = 4		f (X1) = 1.3862 944
X2 = 6		f (X2) = 1.7917 595

Úsese el polinomio para evaluar ln 2

SOLUCIÓN:

Aplicando la ecuación (8) da:

b0 = 0

la ecuación (9) genera:

Coeficiente Lineal

Y la ecuación (10) da:

Coeficiente Cuadrático

Sustituyendo estos valores en la ecuación (4) se obtiene la fórmula cuadrática:

f 2 ( X ) = 0 + 0.4620981 (X - 1) - 0.05187312 (X - 1) (X - 4)

que se evalúa en X = 2 y se obtiene

f 2 ( 2 ) = 0.5658443

Lo que representa un error porcentual del e% = 18.4%. Por lo tanto, mejora la interpolación comparada con los resultados obtenidos al usar una línea recta (ejemplo 3.1).