|
|
|||||||||||||
INTERPOLACIÓNINTRODUCCIÓNCon frecuencia se tienen que estimar valores intermedios entre valores conocidos. El método mas común empleado para este propósito es la interpolación polinomial. Recuerdese que la fórmula general de un polinomio de n-ésimo orden es:
Para n + 1 puntos, existe uno y sólo un polinomio de n-ésimo orden o menor que pasa a través de todos los puntos. Por ejemplo, hay sólo una línea recta (es decir un polinomio de primer orden) que conecta dos puntos. El polinomio de interpolación consiste en determinar el único polinomio de n-ésimo orden que se ajusta a los n + 1 puntos dados. Este polinomio proporciona una fórmula para calcular los valores intermedios. Aunque existe uno y sólo un polinomio de n-ésimo orden que se ajusta a los n + 1 puntos, existen una gran variedad de fórmulas matemáticas mediante las cuales se puede expresar este polinomio. En esta unidad se estudian dos técnicas alternativas que están bien condicionadas para implementarse en una computadora. Estos son los polinomios de Newton y de Lagrange.
POLINOMIOS DE INTERPOLACIÓN
|
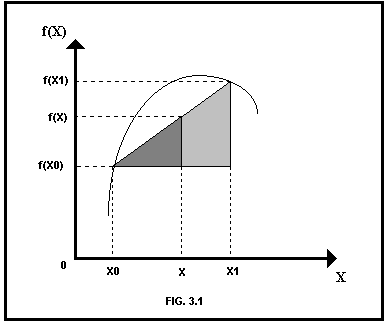
|
Fig. 1
Usando triángulos semejantes, se tiene:
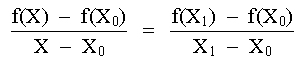
|
(2) |
Que se puede reordenar como:
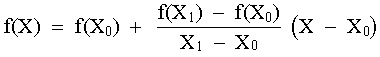
|
(3) |
La cuál es la fórmula de interpolación lineal. La notación f1(X) indica que se trata de un polinomio de interpolación de primer orden. Nótese que además de representar la pendiente de la línea que conecta los dos puntos, el término [ f(X1) - f(X2) ] / (X1 - X2) es una aproximación de diferencias divididas finitas a la primera derivada. En general, entre mas pequeño sea el intervalo entre los puntos, más exacta será la aproximación.
EJEMPLO 3.1
Calcúlese el logaritmo natural de 2 (ln 2) usando interpolación lineal.
Primero, llévese a cabo los cálculos interpolando entre ln 1 = 0 y ln 6 = 1.7917595.
Después repítase el procedimiento, pero usando un intervalo más pequeño desde ln 1 a ln 4 = 1.3862944.
Nótese que el valor real de ln 2 = 0. 69314718
SOLUCIÓN:
Evaluando la fórmula de interpolación lineal (3) de X = 1 a X = 6 da:
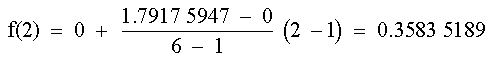
La cual representa un error porcentual de e% = 48.3 %. Usando el intervalo más pequeño desde X = 1 a X = 4 da:
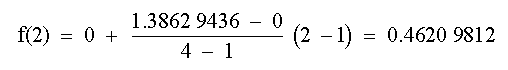
Por lo contrario, usando el intervalo más pequeño reduce el error relativo porcentual a e% = 33.3%.