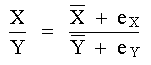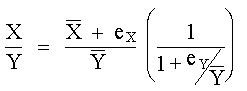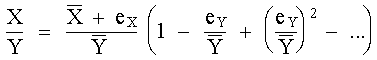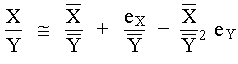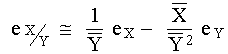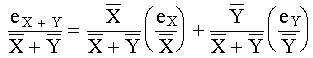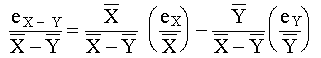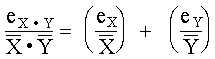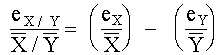TEORÍA DE ERRORES

PROPAGACIÓN DEL ERROR

En una materia como métodos numéricos o en un análisis numérico en que se usa la computadora, es muy importante conocer la propagación del error en algún punto del proceso de cálculo. Y dado que los errores están de alguna manera relacionados con las cantidades y las operaciones que se hacen con ellas, es necesario conocer o encontrar las expresiones para las cuatro operaciones fundamentales, tanto para el error absoluto como para el error relativo en función de dos operandos y sus errores.

SUMA

Se tienen dos aproximaciones, y , a dos valores verdaderos, X y Y, junto con sus errores respectivos, e X y eY.

Tendremos entonces:

(24)

El error en la suma, que indicaremos mediante eX+Y, es por tanto,

RESTA

De una manera semejante obtenemos

MULTIPLICACIÓN

En este caso se tiene

(27)

Suponemos que los errores son mucho mas pequeños que las aproximaciones, e ignoramos el producto de los errores. Entonces:

(28)

y

(29)

DIVISIÓN

Tenemos

(30)

Multiplicando el denominador por y reacomodando términos obtenemos

(31)

El factor en paréntesis puede desarrollarse en serie mediante una división:

(32)

Efectuando la multiplicación y despreciando todos los términos que contienen productos o potencias de orden superior al primero de eX y eY tenemos

(33)

por lo tanto

(34)

Debe observarse que rara vez conocemos el signo de un error. Por ejemplo, no se debe inferir que la suma incrementa siempre el error y que la resta siempre lo disminuye simplemente porque los errores se suman en la adición y se restan en la substracción. Si los errores tienen signos diferentes ocurrirá precisamente lo contrario.

Como tenemos ahora fórmulas para la propagación de los errores absolutos en las cuatro operaciones aritméticas básicas, podemos fácilmente dividir y obtener los errores relativos. Para la suma y la resta los resultados han sido reacomodados para mostrar explícitamente el efecto de los errores en los operandos:

Suma

(35)

Resta

(36)

Multiplicación

(37)

División

(38)