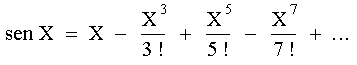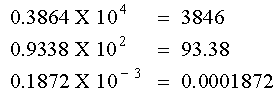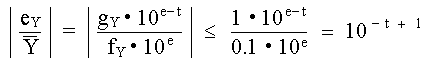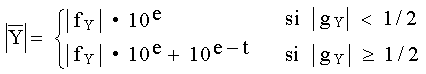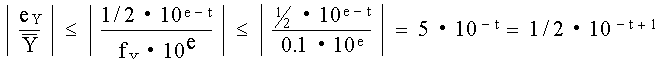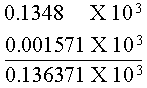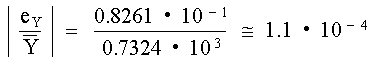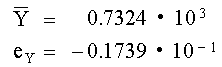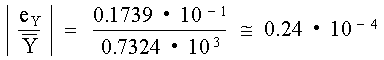|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TEORÍA DE ERRORESERRORES INHERENTES, POR TRUNCAMIENTO Y POR REDONDEOExisten tres tipos básicos de errores en una computación numérica: inherentes, por truncamiento, y por redondeo. Cada uno se puede expresar en forma absoluta o en forma relativa. 1. ERRORES INHERENTESSon errores que existen en los valores de los datos, causados por incertidumbre en las mediciones, por verdaderas equivocaciones, o por la naturaleza necesariamente aproximada de la representación, mediante un número finito de dígitos, de cantidades que no pueden representarse exactamente con el número de dígitos permisible. Por ejemplo, si necesitamos usar p en un cálculo, podemos escribirlo como 3.14, 3.1416, 3.1415926535589793..., etc. En muchos casos aún una fracción simple no tiene representación decimal exacta, por ejemplo 1/3, que puede escribirse solamente como una sucesión finita de números 3. Muchas fracciones que tienen representación finita en un sistema no la tienen en otro, el número 1/10 es igual a 0.1 en decimal y en binario es 0.000110011001100... 2. ERRORES POR TRUNCAMIENTOEstos son debidos a la omisión de términos en una serie que tiene un número infinito de términos. Por ejemplo podemos utilizar la serie infinita de Taylor para calcular el seno de cualquier ángulo X, expresado en radianes:
Por supuesto que no podemos usar todos los términos de la serie en un cálculo, porque la serie es infinita; entonces, los términos omitidos introducen un error por truncamiento. 3. ERRORES POR REDONDEOEstos errores se introducen en los procesos de computación por el hecho de que las computadoras trabajan con un número finito de dígitos después del punto decimal y tienen que redondear. Como nos interesa el redondeo de punto flotante, revisaremos la forma de representación de un número de punto flotante. Recordando que cada número lo podemos representar por una fracción generalmente llamada Mantisa, la cual está multiplicada por una potencia del número base, llamada generalmente el Exponente. Entonces tenemos números como los siguientes:
Se puede determinar un límite al error relativo máximo que puede ocurrir en un resultado aritmético obtenido con redondeo truncado. El error relativo máximo ocurre cuando gY es grande y fY es pequeño. El valor máximo posible de gY es menor que 1.0; el valor mínimo de fY es 0.1, por lo que el valor absoluto del error relativo es:
Entonces se observa que el máximo error relativo por redondeo en el resultado de una operación aritmética de punto flotante no depende del tamaño de las cantidades, sino del valor numérico de dígitos que se manejen.
El tipo mas conocido de redondeo, que se denomina generalmente redondeo simétrico, puede describirse como sigue. Dadas las dos partes de un resultado como en el caso anterior, la aproximación redondeada a Y está dada por:
en que Y tiene el mismo signo que fY. La adición de 10 en el segundo renglón de la ecuación corresponde a sumar 1 al último dígito retenido si el primer dígito que se pierde es igual o mayor que 5. Se describen los símbolos de valor absoluto para indicar que las mismas fórmulas se aplican a cantidades positivas y negativas. Si gY < 1/2, el error absoluto es
Si
De cualquier manera, tenemos 10 multiplicado por un factor cuyo valor absoluto no es mayor que 1/2. El valor absoluto del error absoluto es, por lo tanto
y el valor absoluto del error relativo es entonces
Si f representa la mantisa de un número de punto flotante, y e el exponente podemos expresar en forma general un número de punto flotante en base decimal como:
En donde sabemos que f no puede ser menor que 1/10 puesto que los números han sido normalizados y no puede llegar a ser 1 porque la mantisa es una fracción propia. Ahora si realizamos la suma de los números:
La computadora se encarga de la colocación del punto y compara los exponentes para desplazar hacia la derecha el punto para alinearlos. Entonces para el ejemplo hace lo siguiente:
Así se pueden sumar directamente las dos mantisas. Obviamente, la mantisa de la suma tiene mas de cuatro dígitos. Antes de redondear, el resultado puede mostrarse como dos cantidades de punto flotante:
Cualquier resultado proveniente de la realización de las cuatro operaciones aritméticas puede indicarse, antes de ser redondeado, por la forma general:
en donde t es el número de dígitos de fY. El intervalo de valores posibles de fY es:
y el intervalo de variación de gY es:
Para un ejemplo de la diferencia entre las dos reglas de redondeo, considérese el siguiente resultado de alguna operación aritmética:
Para redondeo truncado
y
( Para la operación que llamamos redondeo simétrico,
y
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||