Recursión

Los programas que se han analizado e implementado hasta el momento están estructurados en general como funciones que llaman unas a otras. Para algunos tipos de problemas, es útil tener funciones que se llamen a sí mismas. Una función recursiva es una función que se llama a sí misma, ya sea directa o indirectamente a través de otra función.

Una función recursiva es llamada para resolver un problema. La función de hecho, sabe sólo cómo resolver el caso más simple, es decir, el llamado caso base. Si la función es llamada con un problema más complejo, la función divide dicho problema en dos partes conceptuales: una parte que la función ya sabe como ejecutar y una parte que la función no sabe como ejecutar.

Para hacer factible la recursión, esta última parte debe parecerse al problema original, la función llama a una copia nueva de sí misma, para que empiece a trabajar sobre el problema más pequeño y esto se conoce como una llamada recursiva y también se llama el paso de recursión.

El paso de recursión también incluye la palabra reservada return, porque el resultado será combinado con la parte del problema que la función supo como resolver para formar un resultado que será regresado al llamador original, posiblemente main.

Como un ejemplo de estos conceptos en operación, escribamos un programa recursivo para ejecutar un cálculo matemático popular.

El factorial de un entero n, se expresa como un conjunto de productos:

n * (n-1) * (n-2) *……* 1

Escribiendo el código en lenguaje C usando el ciclo for es de la siguiente manera:

int i, factorial; 
factorial=1;

for(i=numero;i>=1;i--)
 factorial*= i;

Por ejemplo 5!, claramente es lo mismo que 5*4!, como se muestra mediante el siguiente:

5!=5
5!=5*(4*3*2*1)
5!=5*(4!)

En la figura mostrada a continuación muestra la sucesión de llamadas recursivas continúa hasta que 1! Se evalúa al valor 1, lo que termina la recursión. En la figura del lado derecho se muestran los valores regresados por cada llamada recursiva a su llamador, hasta que el valor final es calculado y regresado.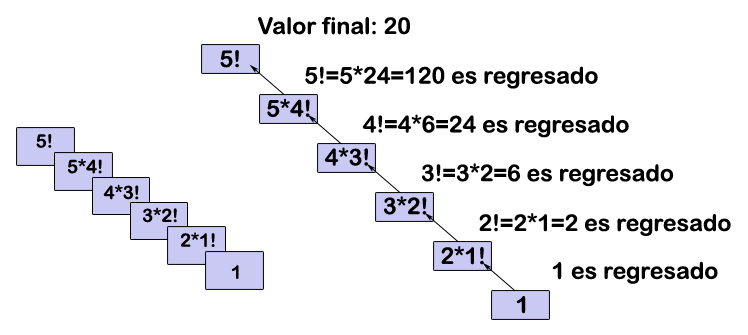

La función recursiva factorial primero prueba para ver si una condición de terminación es verdadera, es decir, es número menor que o igual a 1. Si número es en verdad menor que o igual a 1 factorial regresa 1, ya no es necesaria mayor recursión y el programa termina.

El código sería el siguiente:

using System;
namespace ConsoleApplication14
{
 /// <summary>
 /// Esta clase 
 /// <SUMMARY>
 class factorial
 {
  int numero;
  int fact(int num)
  {
   numero=num;
   if(numero<=1)
    return 1;
   else
    return(numero*fact(numero-1));
  }
  [STAThread]
  static void Main(string[] args)
  {
   factorial f1=new factorial();
   Console.WriteLine("Dame el número para calcular su factorial");
   int p,n;
   n=int.Parse(Console.ReadLine());
   p=f1.fact(n);
   Console.WriteLine("El factorial es:\n");
   Console.Write(p+"\n");
  }
 }
}

Otro ejemplo donde se aplica la recursión son las Torres de Hanoi.

El problema consiste en tres barras verticales A,B,C y n discos de diferentes tamaños, apilados inicialmente en la barra A y se desea pasar los discos a la barra C, conservando su orden.

Las reglas son:

1.- Se moverá un solo disco cada vez.

2.- Un disco no puede situarse sobre otro más pequeño.

3.- Se utilizará la barra B como pila auxiliar.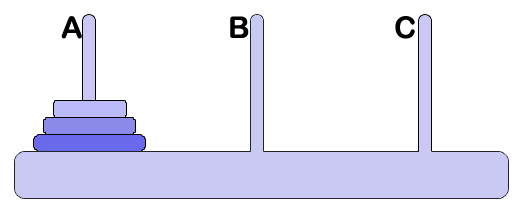

Una posible solución, es el algoritmo recursivo que se muestra a continuación:

1.- Mover n-1 discos de la barra A a la B (el disco n es el del fondo).

2.- Mover el disco n de la barra A a la C.

3.- Mover los n-1 discos de la barra B a la C.

El código sería el siguiente:

class  Nombre de la Clase
{
	///declaración de sus atributos
	///declaración de sus métodos
}

Por ejemplo:

using System;
using System.Collections;
class Hanoi
{
	public static void dex(int ndiscos, Stack origen,Stack destino,Stack auxiliar){
	if(ndiscos < 0)  Console.WriteLine("El numero de discos es incorrecto");
	if(ndiscos == 0)  return;
	if(ndiscos == 1) destino.Push(origen.Pop());
	else{
		dex(ndiscos-1,origen,auxiliar,destino);
		destino.Push(origen.Pop());
		dex(ndiscos-1,auxiliar,destino,origen);
		}
	}
	public Hanoi(int n,Stack a,Stack b,Stack c){
		dex(n,a,b,c);
	}
}
public class hprueba{
	public static void Main(){
		int n=0;
		Console.WriteLine("Bienvenidos a este programa sobre torres de Hanoi\n"
		+"se usan pilas y se ocupa un metodo recursivo llamado\n"+"\tdex");
		Console.WriteLine("Introduce el numero de discos");
			n=int.Parse(Console.ReadLine());
			Stack a=new Stack(n);
		Stack b=new Stack(n);
		Stack c=new Stack(n);
		for(int i=n;i>0;i--)
			a.Push(i);
			Hanoi wow=new Hanoi(n,a,b,c);
		Console.WriteLine("Movimientos: {0}",System.Math.Pow(2,n)-1);
		Console.WriteLine();
		Console.Write("pila destino ");
		foreach(int i in c)
			Console.Write(i+" ");
		Console.WriteLine();
	}
}

Bubble Sort -- Ver Animación

Insertion Sort -- Ver Animación

Quick Sort -- Ver Animación

Selection Sort -- Ver Animación

Shell Sort -- Ver Animación