|
LAS TORRES DE HANOI
Una antigua leyenda dice que en cierto monasterio de Hanoi había tres postes y que en uno de ellos había 64 discos de tamaño decreciente, uno encima de otro y con el mayor hasta abajo. Los monjes del monasterio han estado trabajando sin cesar para llevar los discos desde su poste original hasta algún otro siguiendo una regla sencilla: solamente pueden mover un disco a la vez de un poste a otro, siempre y cuando queda arriba de uno mayor. La leyenda indica que el mundo terminará en el momento en que los monjes hayan logrado su propósito.
Llamemos a los postes A, B y C (siendo A el poste original y C el poste al que queremos mover todos los discos). Si solamente hubiera un disco, la tarea hubiera sido muy sencilla: movamos el único disco del poste A al poste C (y el mundo se hubiera terminado en un santiamén). Si solamente hubieran dos discos, la tarea no hubiera sido mucho más difícil: basta mover el disco pequeño al poste B, después el disco grande al poste C y finalmente el disco pequeño al poste C. Si continuamos de esta manera, pronto nos daremos cuenta que la labor monumental de mover los 64 discos se reduce a la siguiente: movamos los 63 discos más pequeños del poste A al B, movamos el disco más grande del poste A al C y finalmente movamos los 63 discos más pequeños del poste B al C. ¿Cómo hacemos para mover los 63 discos? Lo haremos de la misma forma, excepto que renombrando los postes adecuadamente.
De esta manera, hemos dividido la tarea de mover n discos en dos tareas menores. Así, podemos convencernos de que el siguiente algoritmo recursivo mueve n discos de un poste original a un poste destino utilizando un tercer poste auxiliar, esto es:
Hanoi(n, Original, Auxiliar, Destino)
Comienza
Si n es mayor que 0 entonces
Hanoi(n-1, Original, Destino, Auxiliar)
Mueve un disco de Original a Destino
Hanoi(n-1, Auxiliar, Original, Destino)
Termina
A continuación, se muestra una implementación sencilla de este algoritmo en C# para una aplicación de consola:
using System;
using System.Collections.Generic;
using System.Text;
namespace Torres_de_Hanoi
{
class Hanoi
{
int pasos = 0;
static void Main(string[] args)
{
Hanoi h = new Hanoi();
char TorreInicial='A';
char TorreAuxiliar='B';
char TorreFinal='C';
int n;
String a;
Console.WriteLine("Número de discos: ");
a = Console.ReadLine();
n = int.Parse(a);
Console.WriteLine("\nLos movimientos a realizar son: \n");
h.hanoi(n,TorreInicial,TorreAuxiliar,TorreFinal);
Console.WriteLine("\nEl número total de pasos es: " + h.pasos + "\n");
Console.ReadLine();
}
void hanoi(int n, char c, char a, char f)
{
if(n==1)
{
Console.WriteLine(c + " -> " + f);
pasos++;
}
else
{
pasos++;
hanoi(n-1,c,f,a);
Console.WriteLine(c + " -> " + f);
hanoi(n-1,a,c,f);
}
}
}
}
La secuencia de movimientos que produce este algoritmo es la única solución óptima (es decir, de longitud mínima) posible. El número de movimientos es M(n) = 2^n−1, como se puede demostrar fácilmente por inducción sobre el número de discos.
Se cumple para n = 1
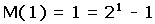
Si se cumple para n, se cumple para n+1.
Al ejecutarse el algoritmo, podemos ver que para n+1, la condición pasa al else y se llama a sí mismo dos veces para n, más un movimiento del disco n+1. Así que:
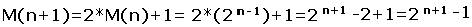
Para n = 8 el número de movimientos es de 28−1 = 255. Para n = 64, el número de movimientos es de 264−1 = 18.446.744.073.709.551.615. Si los monjes cambiaran un disco de sitio cada segundo necesitarían más de quinientos ochenta mil millones de años para terminar su tarea, unas cuarenta veces la edad del Universo.
Los algoritmos recursivos funcionan bien con ordenadores, pero son difíciles de aplicar para un ser humano. Por ejemplo, si intentas resolver la torre de ocho discos aplicando el método descrito es fácil que te pierdas a no ser que vayas tomando notas de por dónde vas.
|